1、原理
1)区域的“奇偶”性质
多边形扫描转换主要依据区域的一种“奇偶”性质,即一条直线与任意封闭的曲线相交时,总是从第一个交点进入内部,再从第二个交点退出,在交替的进入退出过程中对多边形进行填充。
2)活跃边表(Active Edge Table,AET)
用这个表存贮与当前扫描线相交的各边。每次离开一条扫描线进入下一条之前,将表中有但与下一条扫描线不相交的边清除出表,将与下一条扫描线相交而表中没有的边加入表中。AET中总是按x坐标递增排序,因为在进行填充时,需要按该顺序判断是进入多边形内部还是从多边形内部出去。
3)边表(Edge Table,ET)
(1)在对多边形进行填充之前,首先应该建立多边形的边表来存储多边形的边的信息,边表是一种邻接表。ET中各登记项按y坐标递增排序,每一登记项下的“吊桶”按所记x坐标递增排序,“吊桶”中各项的内容依次是:
① 边的另—端点的较大的y坐标ymax。
② 与较小的y坐标对应的边的端点的x坐标xmin。
③ 斜率的倒数,即1/m。

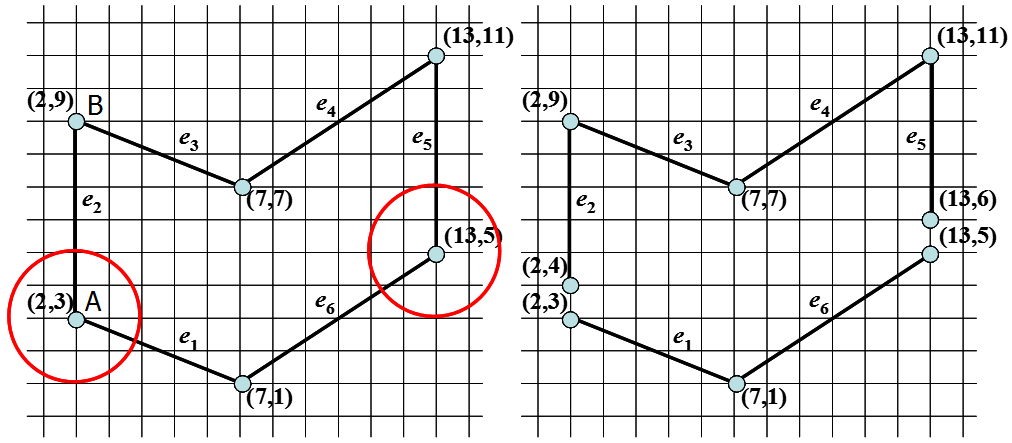
(2)注意:在建立边表时,当顶点表现为是局部极大或局部极小时(下图中的B点),就看做是二个,否则看做一个。实际处理这个问题时,对局部极大或局部极小的顶点无需处理,而其它的顶点应该沿着边的方向缩进一个单位。
理由如下:例如在下图中,对于B点来来说,无需多做处理,因为当扫描线 y=9 时,e2和e3都会包含到AET中,也就是说B点在当前AET中会出现两次,当进行填充时,在该点会完成一次进入和退出,也就不会出现错误填充的情况。而对于A点来说,如果不进行缩进,当扫描线 y=3 时,e1和e2都会包含到AET中,所以A点同样在当前AET中出现两次,此时,AET中有三个点,y=3 这一行上A点之后的多边形内部区域并不会进行填充,发生错误,而且AET中应该永远包含偶数个点才对;进行缩进后,A点在当前AET中只出现一次,并且此时AET中有偶数个点,填充正确。
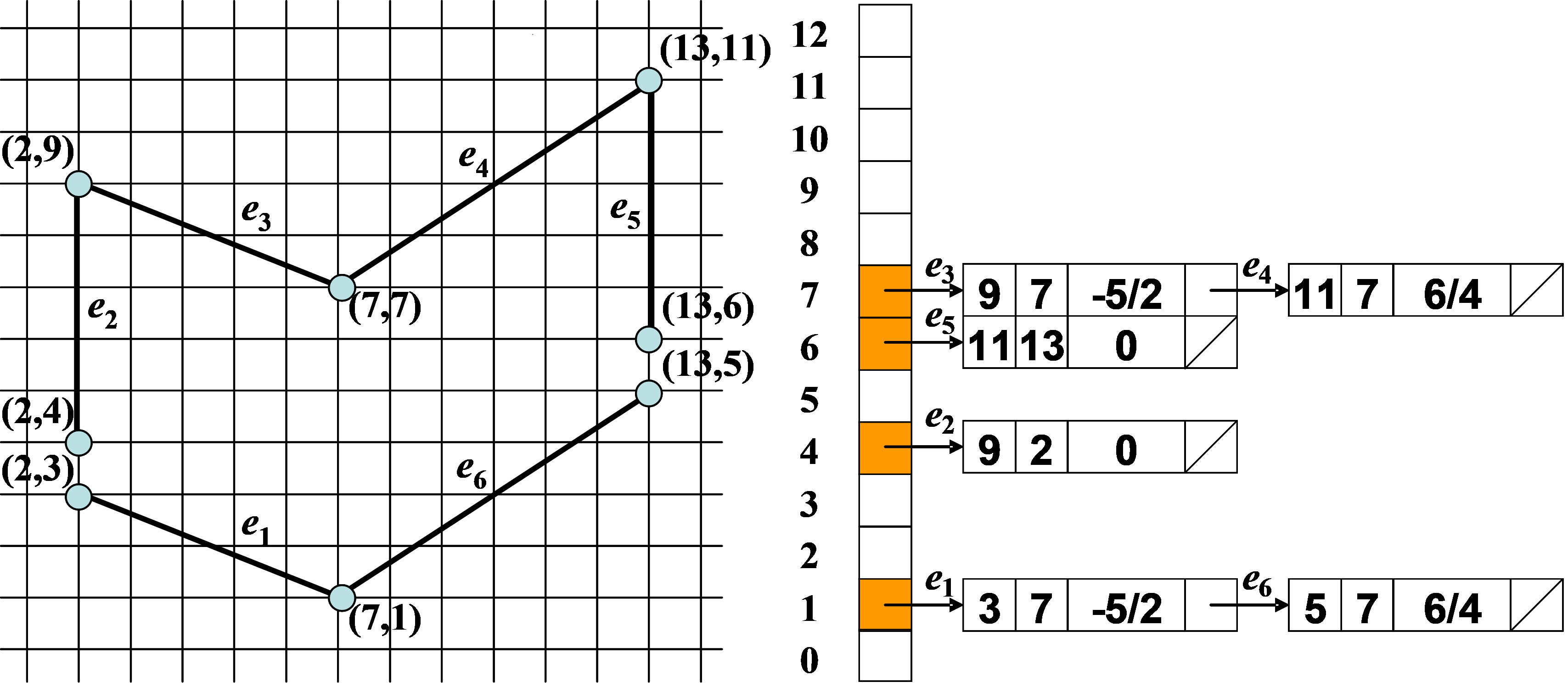
(3)建立好的ET如下所示:
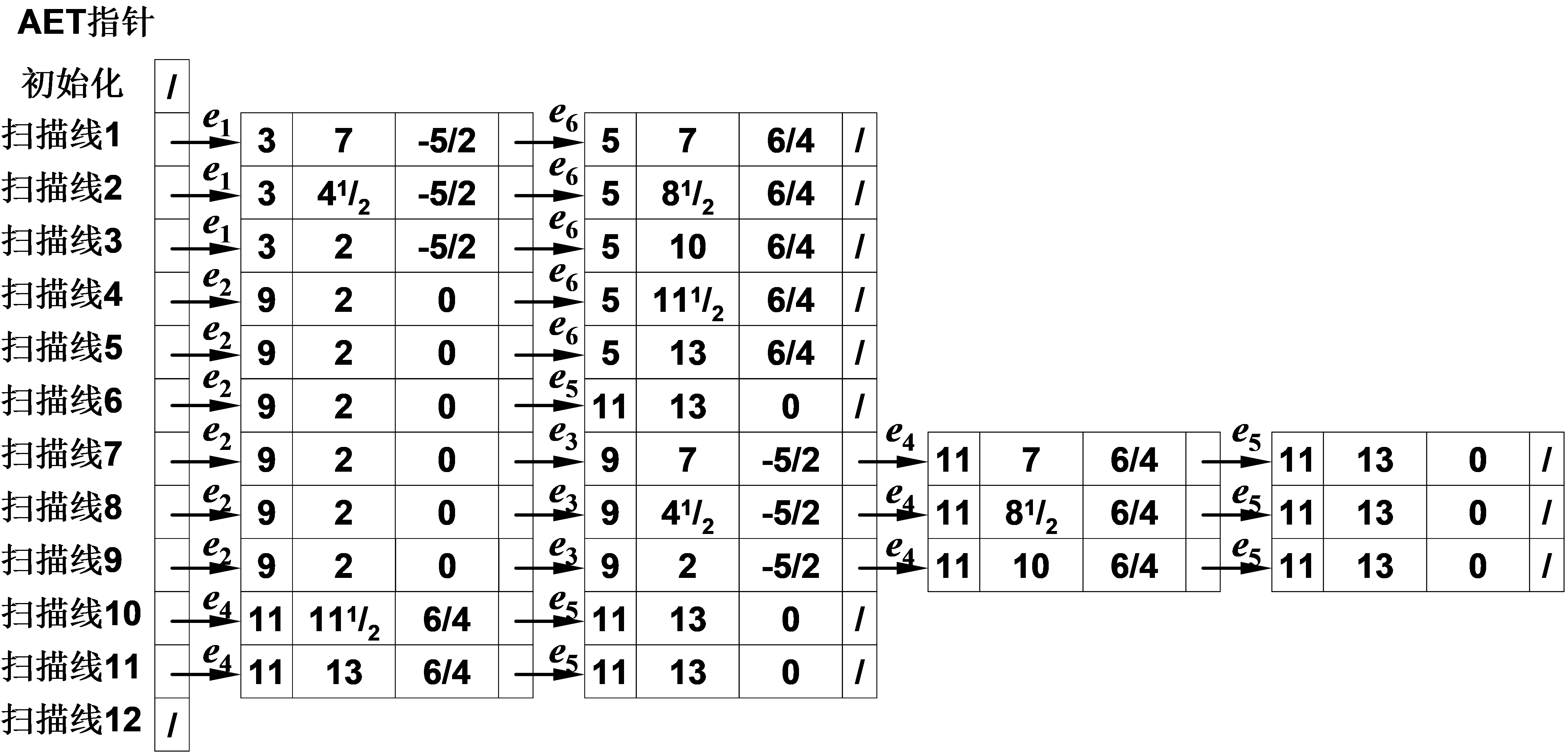
4)扫描过程
5)填充算法的伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void Polygonfill(EdgeTable ET, COLORREF color)
{
1.y=边表ET中各登记项对应的y坐标中最小的值;
2.活跃边表AET初始化为空表;
3. while(ET表中仍有扫描线未被处理)
{
3.1将ET中登记项y对应的各“吊桶”合并到表AET中,
将AET中各吊桶按x坐标递增排序;
3.2在扫描线y上,按照AET表提供的x坐标对,用color实施填充;
3.3将AET表中有y=ymax的各项清除出表;
3.4对AET中留下的各项,分别将x换为x+1/m.
3.5由于前一步可能破坏了AET表中各项x坐标的递增次序,
故按x坐标重新排序;
3.6 y++,去处理下一条扫描线。
}
}
|
2、实践
1)题目要求
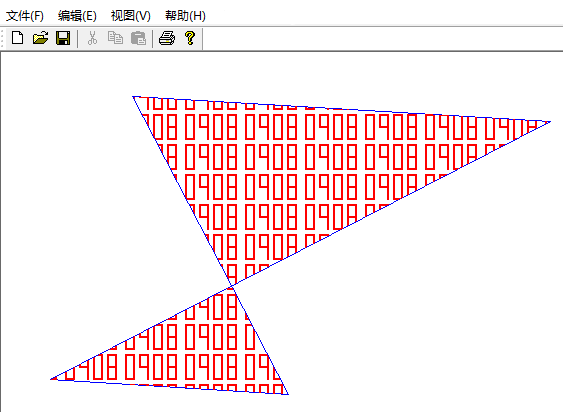
通过鼠标输入顶点的方法绘制多边形,并实现多边形的扫描转换算法完成对该多边形的填充,要求使用“0908”数字图案对多边形内部进行填充,并且多边形边界为蓝色,填充颜色为红色。
2)分析
(1)定义一个30*60的bool型数组m_pattern,用来存储需要填充的“0908”图案,在画像素点(x,
y) 时进行判断,如果m_pattern[y%30][x%60] 为true则进行填充,否则不进行填充。
(2)通过鼠标点击和移动绘制多边形的边,当多边形新绘制的点和第一个点的距离相差5个像素时,认为该多边形绘制完成。并且在绘制过程中完成边表的建立。对顶点进行处理时,取出当前点的前两个点,判断前一个点是否局部极大或局部极小,来决定是否要对前一个点进行缩进;并且在画最后一个顶点(也就是第一个顶点)时,既要判断前一个点是否要进行缩进,也要判断当前点是否要缩进。
(3)当最后一个点按下后,开始进行填充,开始时扫描线y值初始化为边表的第一个值(该值为多边形的最小的y值),之后扫描线逐步向上移动,然后按照边表更新活跃边表,并按区域的“奇偶”性质进行填充。
3)代码实现
(1)构建边表的部分代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
if (m_lastPoint.y != point.y)
{
if (((m_beforLastPoint.y <= m_lastPoint.y) && (point.y <= m_lastPoint.y)) ||
((m_beforLastPoint.y >= m_lastPoint.y) && (point.y >= m_lastPoint.y)))
{
CPoint maxPoint = m_lastPoint.y > point.y ? m_lastPoint : point;
CPoint minPoint = m_lastPoint.y > point.y ? point : m_lastPoint;
pEdge edge = new Edge();
edge->ymax = maxPoint.y;
edge->xmin = minPoint.x;
edge->next = NULL;
edge->dx = (double)(maxPoint.x - minPoint.x) / (maxPoint.y - minPoint.y);
m_ETs.back()->insertEdge(minPoint.y, edge);
}
else
{
pEdge edge = new Edge();
edge->dx = (double)(m_lastPoint.x - point.x) / (m_lastPoint.y - point.y);
edge->next = NULL;
if (m_lastPoint.y > point.y)
{
edge->ymax = m_lastPoint.y - 1;
edge->xmin = point.x;
m_ETs.back()->insertEdge(point.y, edge);
}
else
{
edge->ymax = point.y;
edge->xmin = m_lastPoint.x + edge->dx;
m_ETs.back()->insertEdge(m_lastPoint.y + 1, edge);
}
}
|
(2)多边形的扫描转换算法实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
|
void CTestView::Polygonfill(CDC * pDC, EdgeTable * et, COLORREF color)
{
pDC->SetROP2(R2_COPYPEN);
double y = et->vertexes.front()->ymin;
double ymax = et->vertexes.back()->ymin;
if (m_AET)
{
delete m_AET;
m_AET = NULL;
}
m_AET = new Vertex();
m_AET->edge = NULL;
pVertex tmp1 = NULL, tmp2 = NULL;
pEdge tmp3 = NULL, tmp4 = NULL;
while (m_AET->edge || y <=ymax)
{
tmp1 = m_AET;
tmp2 = et->getVertex(y);
m_AET = new Vertex();
m_AET->edge = NULL;
if (tmp1)
{
tmp3 = tmp1->edge;
while (tmp3)
{
tmp4 = new Edge();
tmp4->next = NULL;
tmp4->dx = tmp3->dx;
tmp4->xmin = tmp3->xmin;
tmp4->ymax = tmp3->ymax;
m_AET->insertEdge(tmp4);
tmp3 = tmp3->next;
}
}
if (tmp2)
{
tmp3 = tmp2->edge;
while (tmp3)
{
tmp4 = new Edge();
tmp4->next = NULL;
tmp4->dx = tmp3->dx;
tmp4->xmin = tmp3->xmin;
tmp4->ymax = tmp3->ymax;
m_AET->insertEdge(tmp4);
tmp3 = tmp3->next;
}
}
if (tmp1)
{
delete tmp1;
tmp1 = NULL;
}
int yvalue = (int)y;
int x1 = 0, x2 = 0;
for (int i = 0; m_AET->getEdge(i); i += 2)
{
x1 = m_AET->getEdge(i)->xmin + 0.5 + 1;
x2 = m_AET->getEdge(i + 1)->xmin + 0.5;
for (; x1 < x2; x1++)
{
if (m_pattern[yvalue % 30][x1 % 60])
{
pDC->SetPixel(x1, yvalue, color);
}
}
}
m_AET->removeEdge(y);
m_AET->addDx();
y++;
}
}
|
4)实现效果